在数据科学艺术的执行中,统计可以说是一个强大的工具。从高层次来看,统计学是利用数学对数据进行分析的学科。基本的可视化(柱状图等)会给受众一些深层的信息,但通过统计,我们可以用一种更富有信息驱动力和更有针对性的方式对数据进行操作。统计中的数学可以帮助我们对数据形成具体的结论,而不仅仅是猜测。
通过统计,我们可以获得更深入、更细致入微的见解,能够了解数据的确切结构,并在此基础上了解如何应用其他数据科学技术来获取更多信息。
今天,我们来看看数据科学家需要掌握的5个基本统计概念及其应用。
统计特征(Statistical Features)
统计特征可能是数据科学中最常用的统计概念。它通常是你在研究数据集时使用的第一种统计技术,包括偏差(bias)、方差(variance)、平均值(mean)、中位数(median)、百分位数(percentiles)等。这很好理解,在代码中也非常容易实现。下图可以说明这些特征。
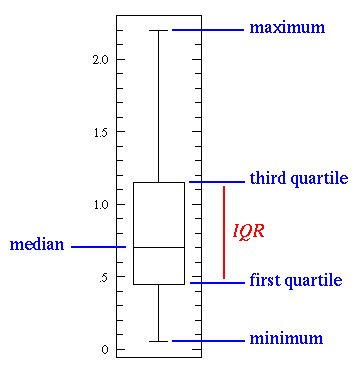
一个基本的箱须图(box- whisker-plot)
中间的那条线是数据的中位数(median),中位数比平均值(mean)更常用,因为它更不容易受到极端数值的影响。第一四分位数(first quartile,Q1)实际上是第25%的数,换句话说,是样本所有数值由小到大排列后第25%的数字。第三四分位数(third quartile,Q3)是第75%的数,即样本所有数值由小到大排列后第75%的数字。上限和下限即样本数据非异常范围内的最大值和最小值。第一四分位数和第三四分位数组成箱须图中的箱子(box plot),第一四分位数-下限以及第三四分位数-上限连接的线段即须(whisker)
箱须图完美地说明了我们可以用基本统计特征得出什么结论:
- 当箱子较短时,意味着样本的数据差别不大,因为在较小范围里有许多值。
- 当箱子较长时,意味着样本的数据差别很大,因为数据分散在较大范围内。
- 如果中位数接近箱子底部,那么就意味着样本中更多数据的数值较小,呈左偏态分布;如果中位数接近箱子顶部,那么就意味着样本中更多数据的数值较大,呈右偏态分布。基本上,如果中位数的那条线不在箱子中间,那么就意味着数据分布偏态。
- “须”很长?这意味着你的样本数据有较高的标准差和方差,换句话说,数据分布分散。如果箱子一边有很长的须,而另一边较短,那么你的数据可能只在一个方向上更为分散。
- 所有这些信息都来自于很容易计算的简单统计特征!当你需要快速获取有意义的数据统计图时,你可以试着画箱须图。
概率分布(Probability Distributions)
概率能够反映随机事件出现的可能性大小。在数据科学中,概率通常被量化在0-1之间,概率为0意味着不可能事件(一定条件下必然不发生的事件),概率为1表示必然事件(一定条件下必然发生的事件)。概率分布是一个函数,表示实验中所有可能值的概率。下图可以帮你理解概率分布。
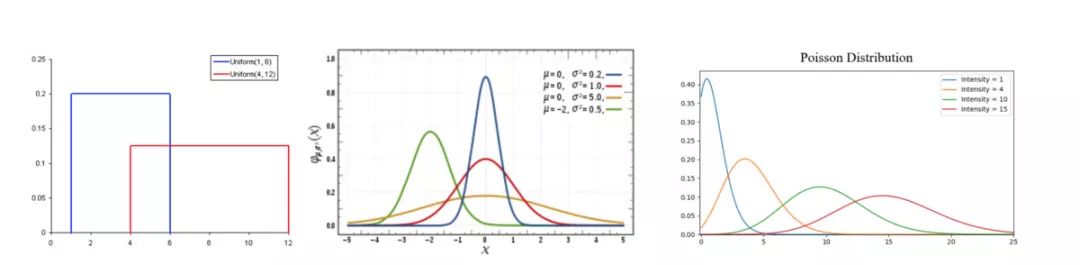
常见的概率分布。
均匀分布(左)、正态分布(中)、泊松分布(右)
- 均匀分布(Uniform Distribution)是3种概率分布中最基本的一种。它在区间内只有一个值,也就是说在相同长度间隔的分布概率是等可能的,范围之外的概率都是0。相当于一个“开或关”的分布。我们也可以把它看作是一个有两个类别的分类变量:0或者那个一定的值。你的分类变量可能有多个值,不仅仅是0,但我们可以把它看作多重均匀分布的分段函数。
- 正态分布(Normal distribution),又称高斯分布(Gaussian Distribution),由其平均值和标准差定义。正态分布的对称轴是样本平均值,随着样本平均值的变化在坐标轴上左右移动,标准差描述了正态分布的离散程度(即数据是广泛分布还是高度集中)。它由平均数所在处开始,分别向左右两侧逐渐均匀下降。与其他分布(如泊松分布)相比,正态分布的标准偏差在所有方向上都是相同的。因此,通过正态分布,我们就可以清楚知道样本的平均值和离散程度。
- 泊松分布(Poisson Distribution)和正态分布相似,但多了偏斜率。如果偏度值非常小,那么泊松分布在各个方向上的分布就和正态分布相似,相对均匀。但当偏度值很大时,数据在不同方向上的分布就不同:在一个方向上,它将非常分散;而在另一个方向上,它将高度集中。泊松分布很适合描述单位时间内随机事件发生的次数。
还得说一句题外话,除了上述三种分布之外,还有其他非常多的概率分布,你都可以深入研究,但这三种分布已经给我们提供了相当多的价值。
我们可以用均匀分布快速查看和解释分类变量。如果看到高斯分布,那我们知道有许许多多算法,它们在默认情况下都会执行地非常优异,我们应该选择它们。对于泊松分布,我们发现必须谨慎地选择一种算法,它拥有足够的鲁棒性应对时空的变量。
维数约简(Dimensionality Reduction)
维数约简这个术语很好理解:有一个数据集,我们想减少它的维度数量。在数据科学中,这个数量是特征变量的数量。维数约简的意义就是降低原来的维数,并保证原数据库的完整性,在约简后的空间中执行后续程序将大大减少运算量,提高数据挖掘效率,且挖掘出来的结果与原有数据集所获得结果基本一致。更广泛的说就是防止了维数灾难的发生。看下图获得更详细的解释:
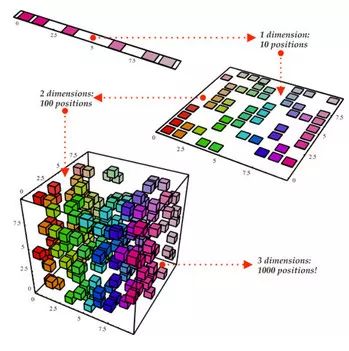
维数约简
立方体代表我们的样本数据集,它有三个维度,共1000个点。以现有的计算能力,1000个点很容易就能处理,但处理更大范围的数据还是会遇到问题。然而,仅仅从二维的角度来看数据集,比如从立方体的一侧来看,我们可以看到区分所有的颜色还是很容易的。通过维数约简,我们可以将三维数据投射(project)到二维平面上。这把我们需要计算的点数减少到100,有效地节约了大量的计算时间。
另一种维数约简的方式是特征修剪(feature pruning)。利用特征修剪,我们基本可以删去对我们的分析不重要的特征。例如,研究一个数据集之后,我们可能发现该数据集有10个特征,其中,有7个特征与输出有很高的相关性,而其余3个相关性不高。那么这3个低相关性特征可能就不值得计算了,我们可以在不影响输出的情况下从分析中删掉它们。
最常用的维数约简方法是主成分分析(PCA),本质上是创建新的向量,这些向量可以尽可能多地反映原始变量的信息特征(即它们的相关性)。
PCA可用于上述两种维数约简方式。在这个教程中可以获得更多相关信息。
过采样和欠采样(Over and Under Sampling)
过采样和欠采样是用于分类问题的统计技术。有时,分类数据集可能过于偏向于一边。例如,类别1有2000个样本,类别2只有200个。我们能够用来建模、预测的许多机器学习技术都没法用了!但是,过采样和欠采样可以解决这个问题。请看这张图:
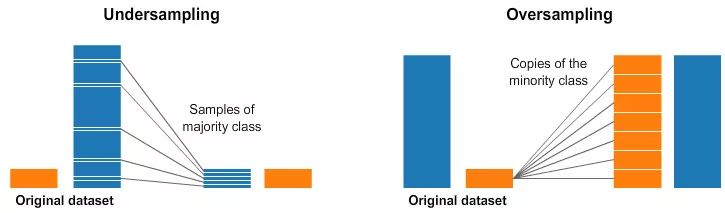
欠采样(左)和过采样(右)
上图里,两张数据图中蓝色类别的样本比橙色多多了。在这种情况下,我们有两个预处理选项,可以帮助训练我们的机器学习模型。
欠采样意味着我们从多数类中选择一些数据,只使用和少数类数量一致的样本。这种选择不是随便挑选的,而是要保证类的概率分布不变。这很容易!我们选取少量样本,使样本数据集更加均匀。
过采样意味着创建少数类样本的副本,使少数类与多数类拥有数量一致的样本。副本创建需要保证少数类的概率分布不变。我们不需要收集更多的样本就能使样本数据集更加均匀。
贝叶斯统计(Bayesian Statistics)
想要完全理解为什么我们要用贝叶斯统计,首先需要理解频率统计(Frequency Statistics)的缺陷。频率统计是大多数人听到“概率”一次时首先会想到的一种统计类型,频率统计检测一个事件(或者假设)是否发生,它通过长时间的试验计算某个事件发生的可能性(试验是在同等条件下进行的),唯一计算的数据是先验数据(prior data)。
可以看这个例子。假如我给你一个骰子,问你掷出6的几率是多少。大多数人会说是1/6。确实如此,如果做频率分析,某人抛掷骰子10000次,计算每个数字出现的频率,那么我们可以看到结果每个数字出现的频率大约是1/6。
但如果有人告诉你,给你的骰子不那么规整,总是6朝上呢?由于频率分析只考虑了之前的数据,上述分析中,骰子不规整的因素没有被考虑进去。
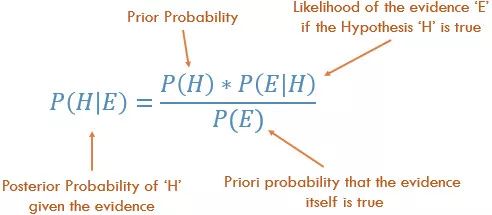
而贝叶斯统计就考虑了这一点。我们可以用下图的贝叶斯法则(Baye’s Theoram)来说明:
贝叶斯法则
方程中,H代表一个事件,E代表另一个,P即某事件发生的概率。
P(H)即先验概率,基本上就是数据分析的结果,即之前事件H发生的概率。
P(E|H)被称作相似度,指假设事件H成立时,事件E发生的概率。
P(E)指事件E成立的先验概率,也被称作标准化常量。
P(H|E)即后验概率,指E发生后,发生H的概率。
例如,如果你想投掷骰子10000次,前1000次全掷出的是6,你很怀疑骰子不规整了。如果我告诉你骰子确实不规整,你是相信我,还是认为这是个骗局呢?
如果频率分析没有什么缺陷,那么我们会比较自信地认定接下来的投掷出现6的概率仍是1/6。而如果骰子确实不规整,或是不基于其自身的先验概率及频率分析,我们在预测接下来数字出现的概率时,就必须要考虑到骰子的因素。当我们不能准确知悉一个事物的本质时,可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。正如你从方程式中能能看到的,贝叶斯统计把所有因素都考虑在内了。当你觉得之前的数据不能很好地代表未来数据和结果的时候,就应该使用贝叶斯统计。
作者|George Seif
原题|The 5 Basic Statistics Concepts Data Scientists Need to Know
源自|towardsdatascience.com
转自|36Kr
更多阅读: